Las Derivadas

Las Derivadas

En cálculo diferencial y análisis matemático, la derivada de una función es la razón de cambio instantánea con la que varía el valor de dicha función matemática, según se modifique el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por eso se habla del valor de la derivada de una función en un punto dado.

Un ejemplo habitual aparece al estudiar el movimiento: si una función representa la posición de un objeto con respecto al tiempo, su derivada es la velocidad de dicho objeto para todos los momentos. Un avión que realice un vuelo transatlántico de 4500 km entre las 12:00 y las 18:00, viaja a una velocidad media de 750 km/h. Sin embargo, puede estar viajando a velocidades mayores o menores en distintos tramos de la ruta. En particular, si entre las 15:00 y las 15:30 recorre 400 km, su velocidad media en ese tramo es de 800 km/h. Para conocer su velocidad instantánea a las 15:20, por ejemplo, es necesario calcular la velocidad media en intervalos de tiempo cada vez menores alrededor de esta hora: entre las 15:15 y las 15:25, entre las 15:19 y las 15:21.

Entonces el valor de la derivada de una función en un punto puede interpretarse geométricamente, ya que se corresponde con la pendiente de la recta tangente a la gráfica de la función en dicho punto. La recta tangente es, a su vez, la gráfica de la mejor aproximación lineal de la función alrededor de dicho punto. La noción de derivada puede generalizarse para el caso de funciones de más de una variable con la derivada parcial y el diferencial.

Definiciones de la derivada

En terminología clásica, la diferenciación manifiesta el coeficiente en que una cantidad ${\displaystyle y\,}$ cambia a consecuencia de un cambio en otra cantidad ${\displaystyle x\,}$.

En matemáticas, coeficiente es un factor multiplicativo que pertenece a cierto objeto como una variable, un vector unitario, una función base, etc.

En física, coeficiente es una expresión numérica que mediante alguna fórmula determina las características o propiedades de un cuerpo.

En nuestro caso, observando la gráfica de la derecha, el coeficiente del que hablamos vendría representado en el punto ${\displaystyle P\,}$ de la función por el resultado de la división representada por la relación ${\displaystyle \textstyle {\frac {dy}{dx}}}$, que como puede comprobarse en la gráfica, es un valor que se mantiene constante a lo largo de la línea recta azul que representa la tangente en el punto ${\displaystyle P\,}$ de la función. Esto es fácil de entender puesto que el triángulo rectángulo formado en la gráfica con vértice en el punto ${\displaystyle P\,}$, por mucho que lo dibujemos más grande, al ser una figura proporcional el resultado de ${\displaystyle \textstyle {\frac {dy}{dx}}}$ es siempre el mismo.

Esta noción constituye la aproximación más veloz a la derivada, puesto que el acercamiento a la pendiente de la recta tangente es tanto por la derecha como por la izquierda de manera simultánea.

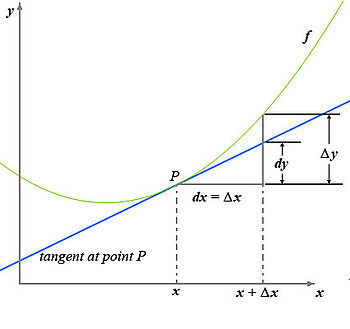
Límite como coeficiente de Diferencias

La derivada de una función ${\displaystyle f\,}$ es la pendiente geométrica de la recta tangente del gráfico de ${\displaystyle f\,}$ en ${\displaystyle x\,}$. Sin el concepto que se va a definir, no es posible encontrar directamente la pendiente de la línea tangente a una función dada, porque solamente se conoce un punto en la línea tangente: ${\displaystyle (x,f(x))\,}$. La idea es aproximar la línea tangente con múltiples líneas secantes que tienen distancias progresivamente más pequeñas entre los dos puntos que cruzan. Cuando se toma el límite de las pendientes de las líneas secantes de esta progresión, se consigue la pendiente de la línea tangente. Se define, pues, la derivada tomando el límite de la pendiente de las líneas secantes, al acercarlas a la línea tangente. Para encontrar las pendientes de las líneas secantes próximas, se elige un número ${\displaystyle h\,}$ relativamente pequeño. ${\displaystyle h\,}$ representa un cambio relativamente pequeño en ${\displaystyle x\,}$, el cual puede ser positivo o negativo. La pendiente de la recta que pasa por los dos puntos ${\displaystyle (x,f(x))\,}$ y ${\displaystyle (x+h,f(x+h))\,}$ es:

${\displaystyle Q(h)={f(x+h)-f(x) \over h}}$.

expresión denominada «cociente de Newton».

Derivada de una Función

Considerando la función f definida en el intervalo abierto I y un punto a fijo en I, se tiene que la derivada de la función f en el punto ${\displaystyle a\,}$ se define como sigue:

${\displaystyle f'(a)=\lim _{h\rightarrow 0}{\frac {f(a+h)-f(a)}{h}}}$,

si este límite existe, de lo contrario, ${\displaystyle f'}$, la derivada, no está definida. Esta última expresión coincide con la velocidad instantánea del movimiento continuo uniformemente acelerado en cinemática.

Aunque podrían calcularse todas las derivadas empleando la definición de derivada como un límite, existen reglas bien establecidas, conocidas como teoremas para el cálculo de derivadas, las cuales permiten calcular la derivada de muchas funciones de acuerdo a su composición sin tener que calcular forzosamente el límite. Tales reglas son consecuencia directa de la definición de derivada y de teoremas anteriores de límites.

También puede definirse alternativamente la derivada de una función en cualquier punto de su dominio de la siguiente manera:

,

La cual representa un acercamiento de la pendiente de la secante a la pendiente de la tangente ya sea por la derecha o por la izquierda según el signo de ${\displaystyle a\,}$. El aspecto de este límite está relacionado más con la velocidad instantánea del movimiento uniformemente acelerado que con la pendiente de la recta tangente a una curva.

No obstante su aparente diferencia, es posible demostrar que el cálculo de la derivada con cualquiera de los límites anteriormente expresados, proporciona siempre el mismo resultado.

Desigualdades

Desigualdades

Desigualdad matemática es una proposición de relación de orden existente entre dos expresiones algebraicas conectadas a través de los signos: desigual que ≠, mayor que >, menor que <, menor o igual que ≤, así como mayor o igual que ≥, resultando ambas expresiones de valores distintos.

Por tanto, la relación de desigualdad establecida en una expresión de esta índole, se emplea para denotar que dos objetos matemáticos expresan valores desiguales.

Algo a notar en las expresiones de desigualdad matemática es que, aquellas que emplean:

• mayor que >
• Menor que <
• Menor o igual que ≤
• Mayor o igual que ≥ 

Estas son desigualdades que nos revelan en qué sentido la una desigualdad no es igual. Ahora bien, los casos de aquellas desigualdades formuladas como:

• Menor que <
• Mayor que >

Son desigualdades conocidas como desigualdades “estrictas”.

En tanto, que los casos de desigualdades formuladas como:

• Menor o igual que ≤
• Mayor o igual que ≥ 

Son desigualdades conocidas como desigualdades “no estrictas o más bien, amplias”.

La desigualdad matemática es una expresión que está formada por dos miembros. El miembro de la izquierda, al lado izquierdo del signo igual y el miembro de la derecha, al lado derecho del signo de igualdad. Veamos el ejemplo siguiente:

3x + 3 < 9

La solución del enunciado anterior nos revela el planteamiento de desigualdad de las expresiones.

Desigualdades e Intervalos

Ahora sabemos que una desigualdad es una expresión algebraica relacionada por signos, y nos sirve para establecer la relación entre 2 cantidades semejantes.

Un intervalo es el conjunto de valores que puede tomar la variable dependiente y que están comprendidos ente dos de ellos ("a" y "b"), que se denominan como extremos del intervalo. La diferencia entre ambos extremos se conoce como "Amplitud del Intervalo" y es igual al valor absoluto de su diferencia |a-b| 

Notación del Intervalo                                                Notación para la Variable
[a,b]                                                                               a<x<b

Puestos en una recta real, los valores a y b se denominan entremos del intervalo. Resolver una desigualdad significa enconrar todos sus soluciones, es decir, obtener el intervalo donde la relacion es verdadera

Propiedades de las Desigualdades

Las siguientes son las propiedades de las desigualdades para los números reales . Están cercanamente relacionadas a las propiedades de igualdad, pero hay diferencias importantes.

Dese cuenta especialmente que cuando multiplica o divide ambos lados de una desigualdad por un número negativo, debe invertir la desigualdad.

Transitividad

Para numeros reales arbitrarios a, b y c:

Si a > b y b > c entonces a > c

Si a < b y b < c entonces a < c

Si a > b y b = c entonces a > c

Si a < b y b = c entonces a < c

Adicion y sustraccion

Para numeros reales arbitrarios a, b y c:

Si a < b entonces a + c < b + c y a - c < b - c

Si a > b entonces a + c > b + c y a - c > b - c

Multiplicacion y divicion

Para números reales arbitrarios a y b, y c diferente de 0:

Si c es positivo y a < b entonces ac < bc y a/c < b/c

Si c es negativo y a < b entonces ac > bc y a/c > b/c 

Opuesto

Para números reales arbitrarios a y b:

Si a < b entonces -a > -b

Si a > b entonces -a < -b

Recíproco

Para numeros reales, a y b distintos son 0, ambos positivos o negativos a la vez:

Si a < b entonces 1/a > 1/b

Si a > b entonces 1/a < 1/b

Si a y b son de distinto signo:

Si a < b entonces 1/a < 1/b

Si a > b entonces 1/a > 1/b

Desigualdades entre medias, notación encadenada y cuerpo ordenado

a) Desigualdades entre Medias:

En matemáticas, se conoce como desigualdad entre media aritmética y geométrica, o MA-MG, aquella desigualdad que establece que la media aritmética de un conjunto de números reales positivos es mayor o igual que la media geométrica del mismo conjunto, cumpliéndose únicamente la igualdad cuando todos los elementos del conjunto sean iguales.

La media aritmética de un conjunto de números reales ${\displaystyle {x_{1},x_{2},\dots ,x_{n}}}$ es igual a la suma dividida por el número total de elementos,

${\displaystyle {\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}.}$

La media geométrica de un conjunto de reales no negativos ${\displaystyle {x_{1},x_{2},\dots ,x_{n}}\in \mathbb {R} ^{+}}$, es igual a la raíz enésima del producto de todos ellos:

${\displaystyle {\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}.}$

Sea ${\displaystyle {x_{1},x_{2},\dots ,x_{n}}\in \mathbb {R} ^{+}}$ entonces

${\displaystyle {\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\geq {\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}.}$

La igualdad se cumple si y sólo si ${\displaystyle {x_{1}=x_{2}=\cdots =x_{n}}}$.

b) Notación Encadenada:
La notación a <> establece que a <>a <> es equivalente a a - e <>.

Esta notación se puede extender a cualquier número de términos: por ejemplo, a1 ≤ a2 ≤ ... ≤ an establece que ai ≤ ai+1 para i = 1, 2, ..., n−1. Según la propiedad de la transitividad, esta condición es equivalente a ai ≤ aj para cualquier 1 ≤ i ≤ j ≤ n.

Ocasionalmente, la notación encadenada se usa con inecuaciones en diferentes direcciones. En ese caso el significado es la conjunción lógica de las desigualdades entre los términos adyacentes. Por ejemplo, a <> c ≤ d significa que a <> c, y c ≤ d. Aparte del uso poco frecuente en matemáticas, esta notación existe en unos pocos lenguajes de programación tales como Python.

c) Cuerpo Ordenado:
En matemáticas, un cuerpo ordenado (también campo ordenado) es un cuerpo con un orden total de sus elementos que es compatible con las operaciones del cuerpo. Un cuerpo ordenado tiene necesariamente la característica 0, puesto que los elementos 0 < 1 < 1 + 1 < 1 + 1 + 1 <... son necesariamente todos distintos. 

Así, un cuerpo ordenado contiene necesariamente un número infinito de elementos: un cuerpo finito no puede ser ordenado.Los cuadrados son necesariamente no negativos en un cuerpo ordenado. Esto implica que los números complejos no pueden ser ordenados ya que el cuadrado de la unidad imaginaria i es -1. Cada cuerpo ordenado es un cuerpo formalmente real.

Espero que este blog los haya ayudado a entender un poco mas acerca de las desigualdades y las relaciones que mantiene con distintas areas de las matematicas.